Says Marty Ross …

Fractions are the easy numbers. Well, comparatively. True, they’re not as easy as whole numbers, 7 and 12 and the like, but there’s nothing too scary about 1/2 or 5/6. Even a fraction within a fraction, such as 1 + 1/(2 + 1/2) for instance, is more bark than bite; a little once-familiar arithmetic can show that this nested mess equals 1 + 2/5 or, if you prefer, 7/5.

But what if we keep going? What if we keep nesting, making a fraction within a fraction within a fraction, and so on, forever:

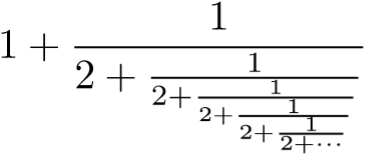
Or, to make it as simple as possible, let’s just use 1s:

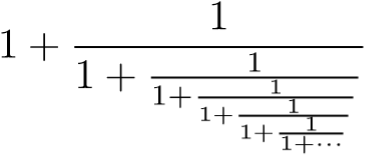
Who would do such a thing? And, why?

Well, the ‘who’ is easy to answer: this is exactly the kind of absurd stunt that mathematicians love to pull, and which so endears them to everyone else. It also suggests an explanation for the ‘why’: to a large extent mathematicians do these absurd things just because they can. Mathematicians find simple joy in stretching ideas as far as they’ll go, all the way to infinity if possible. But it turns out that there is also a surprisingly practical reason to create continued fractions, which is what monsters such as the above are called.

Apart from the easy, fraction numbers there are extremely difficult numbers, the irrational numbers – literally not-ratios, not-fractions. Famous examples of irrational numbers are square roots such as √2, the super-famous π, and the much misunderstood golden ratio, denoted by the Greek letter φ (pronounced as either ‘fie’ or ‘fee’). Such irrational numbers are unavoidable. Square roots arise naturally in right-angled triangles courtesy of Pythagoras’s theorem, φ appears in a similarly polygonal manner, and of course π is a fundamental circle thing.

Now, triangles and circles and the like don’t appear to be all that difficult, suggesting that irrational numbers might be similarly benign. The problem, however, is that although irrational numbers may be accompanied by an easy geometric picture, as numbers they are a mysterious mess. As a typical example, √2 is written in familiar decimals as 1.4142···, where the dots stand for ‘God knows what comes next’. Really. No one knows all the digits that should be where those dots are. Similarly, the golden ratio is in the end just another square root thing, with φ = (1 + √5)/2, which equals 1.6180···. And, π = 3.1415···, including the same ‘God knows’ dots.

What to do.

It turns out what to do is to make continued fractions. Although they look very strange to us now, continued fractions were once very well known, exactly because they make much easier sense of irrational numbers. The first continued fraction above, for example, exactly equals √2. And, the second continued fraction is exactly the golden ratio, φ. Which is about as absurdly beautiful as you can get. There is lots of nonsense written about the golden ratio: φ is not hidden in the human body, φ is not the key to proportional beauty, and φ is not many, many other things. But, as a mathematical creature, φ really is wonderful, and its continued fraction is a stunning thing. (The sorting out of π is another story, which is best left to accompany a future poem.)

Now, are continued fractions an improvement over decimals? You would be forgiven for doubting so, and in particular there are still those troubling dots at the end. But the key point is that the dots don’t necessarily have to be ‘God knows’ dots. For example, all the subsequent stages of the √2 continued fraction above follow the exact same pattern: replace the dots by +1/(2 + ···) at the bottom, in the bottom-most denominator. The golden ratio expression is even simpler: it’s just 1s all the way down.

For mathematicians, and for many others, these expressions for irrational numbers are stunningly beautiful, infinitely more beautiful than ‘God knows’ dots.